Jeudi 19 juin 2025 à 20 heures
« Voyage dans la géométrie de l'espace-temps,
deuxieme saison : la relativité générale »
Stéphane Collion, pilote de ligne, mathématicien
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
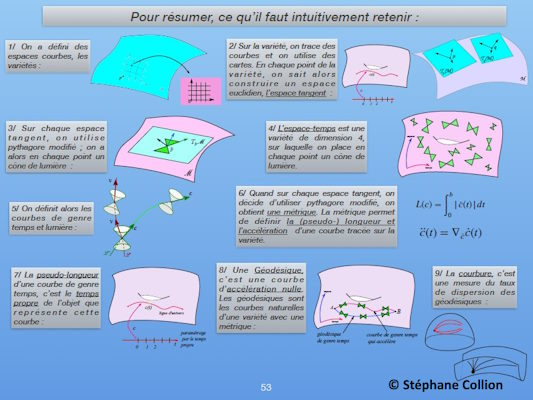
La relativité générale d’Einstein est une des deux grandes
théories de la physique du XX-ème siècle. Mais pour les mathématiciens,
elle apparait surtout comme une théorie d’une élégance formelle sans égale,
proposant de formidables défis mathématiques. En particulier, la relativité
se fonde sur une géométrie aux propriétés distinctes de celle d’Euclide,
sources de phénomènes déroutants tel le paradoxe des jumeaux.
Nous vous proposons une promenade détendue dans les splendides
paysages de cette géométrie pour découvrir que les mathématiques
sont une des sources d’inspiration les plus fécondes des physiciens théoriciens.
Du jeudi 12 au dimanche 15 juin 2025 : « 26ème Salon du CIJM »
Le Salon Culture et Jeux Mathématiques a eu lieu Place Saint-Sulpice (Paris 6ème)
avec pour thème : « Maths hors les murs »
Nos animateurs sont intervenus dans l'espace « Rencontres » du salon :
- Samedi 14 juin de 10h à 11h
- Hervé Stève
- « Homo mathematicus :
- apprendre & comprendre les maths »
« Homo mathematicus » c'est se poser la question de qu’est-ce qu’un.e mathématicien.ne ?
Mais alors comment comprendre et apprendre les maths ? Nous essaierons d’y répondre
à partir de plusieurs notions essentielles qui vont de l’imitation en passant par le doute
jusqu’à l’intuition, tout en essayant de sortir de nombreux clichés tenaces comme celui de la bosse des maths.
ou ont proposé des ateliers sur notre stand :
- Jeudi 12 juin de 11h à 11h30
- Vendredi 13 juin de 11h à 11h30
- Dimanche 15 juin de 15h à 15h30
- Christian Dufour
- « Le principe d'inclusion-exclusion »
Le principe d'inclusion-exclusion est une formule de dénombrement des éléments de l'union d'une famille d'ensembles, dont certains ont une intersection non vide ... Cette formule permet, en excluant les "chevauchements", de ne pas surévaluer le nombre total d'éléments de l'union. Ce principe est employé notamment pour évaluer la fiabilité des réseaux d'ordinateurs. * * * Niveau : 1ère/terminale
- Jeudi 12 juin de 15h à 15h30
- Vendredi 13 juin de 15h à 15h30
- Samedi 14 juin de 15h à 15h30
- Jean Gagnerault
- « Quel calcul pour la date ? »
On s'intéresse au jour de la semaine pour le calendrier grégorien.
Avec quelques congruences, nous proposons de trouver mentalement le jour
de la semaine correspondant à une date donnée.
* * * Niveau : Lycée, Grand public
Jeudi 15 mai 2025 à 20 heures
« Comment mesurer l'efficacité collective
de l'équipe de France de rugby à XV »
Avner Bar-Hen, mathématicien
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
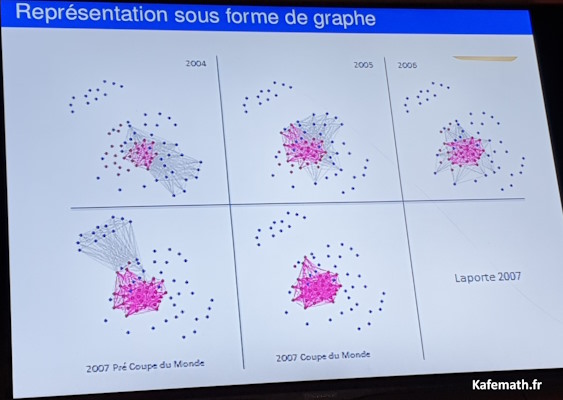
La performance en rugby repose de facto sur les qualités physiques telles que force, vitesse et puissance ainsi que sur les qualités techniques et tactiques, pour autant la pluralité de ces paramètres reste au service de l'efficacité collective. Si l'expérience de jeu est un indicateur qui a été relié à la performance et au succès dans le rugby à XV, la plupart du temps cette dernière est appréhendée individuellement. L'efficacité collective n'est que très peu abordée. L'objectif de cette étude est d'analyser l'ensemble de tous les matchs du XV de France afin de mesurer l'impact du nombre de sélections des joueurs et de leur habitude à jouer ensemble sur l'issue des rencontres..
Jeudi 10 avril 2025 à 20 heures
« Persistances d'un nombre entier »
Blandine Sergent, membre de l'association Kafemath
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
Du calcul de chemin de vie aux erreurs de démonstrations en mathématiques en passant par des mathématiciens et différentes persistances d'un nombre entier.
Jeudi 13 mars 2025 à 20 heures
« La semaine des Maths au Kafemath ! »
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
En avant-première, une célébration de la journée du 03/14 :
« Le Kafemath V.I.Pi »
par Marie-Francoise Dela𝛑erre
Miniatures : petits exposés proposés par des membres de Kafemath
Hervé Stève :
« Zêta de 3 : la constante d'Apéry »
C'est avec une certaine surprise que Roger Apéry prouve en 1978 l'irrationnalité de la somme des inverses des cubes des entiers.
Jean Gagnerault :
Le magicien révèle le nombre choisi par un spectateur.
Christian Dufour :
« Petite promenade chez les Automathes »
Bref rappel sur les automates, suivi de quelques exemples simples.
Gilles Moine :
Cédric Tolédano :
Un classement basé sur les probabilités de gain entre les joueurs.
Les probabilités de gain étant estimées à partir des parties passées.
Exemple :
Si A a 1 chance / 3 de gagner contre B (probabilité de gain : 1/3)
et B a 1 chance / 3 de gagner contre C
Quelle est la probabilité que A gagne contre C ?
François Lavallou :
Les formules de Héron et Pythagore avec les mains, les doigts dans le nez et sans prise de tête. C'est le pied!
Jean-Jacques Dupas :
François Dubois :
On la connaît tous... mais comment l'expliquer avec les mains ?
Jeudi 13 février 2025 à 20 heures
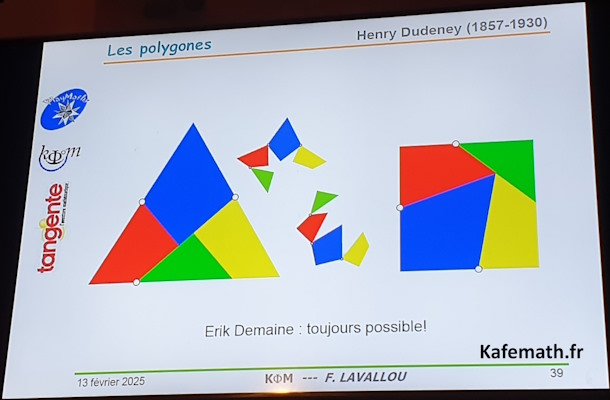
« Les polygones »
François Lavallou, membre de l'association Kafemath
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
Les polygones sont le parangon des sujets qu'il serait prétentieux de dire triviaux, et appellent à une naturelle modestie mathématique tant le contraste est grand entre leur apparente simplicité et la richesse de leurs propriétés.
Jeudi 30 janvier 2025 à 20 heures
« Avez-vous des (hyper) complexes ? »
Hervé Stève, ingénieur mathématicien dans l'aéronautique, co-fondateur du Kafemath
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
Les nombres hypercomplexes sont des éléments d’algèbre qui sont une extension de
l’arithmétique des nombres complexes, ayant des applications récentes en mécanique
quantique, pour la physique relativiste, l’informatique et les mathématiques.
Pour comprendre ces nombres, nous revisiterons l’algèbre des nombres réels
puis celle des complexes exprimables en dimension 2. Devant l’impossibilité
de créer une algèbre pour la dimension 3, en 1843, un mathématicien irlandais,
William Rowan Hamilton, invente les quaternions, des nombres nouveaux pour la
dimension 4. Nous montrerons comment cette innovation permettra de populariser
ces nombres en ouvrant à d’autres extensions qui sont les hypercomplexes.
Jeudi 16 janvier 2025 à 20 heures
« Phénomènes insolites dans la structure multiplicative des entiers »
Jean-Marie De Koninck, Professeur de mathématiques, Université Laval (Québec)
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
Si on énumère les plus grands facteurs premiers des entiers positifs inférieurs à x=100 millions, quel est le nombre premier p qui apparait le plus souvent? C’est p=199. Il va de soi que ce nombre va en grandissant lorsqu’on choisit un x de plus en plus grand. De même, on peut se demander quel est le nombre premier p qui apparait le plus souvent comme deuxième plus grand facteur premier des entiers positifs inférieurs à 100 millions. Étonnamment, c’est p=3, et il en est de même si on remplace 100 millions par 100 milliards. Dans cet exposé, nous mettrons en évidence une variété de phénomènes contre-intuitifs qui rendent fascinante l’étude de la structure multiplicative des entiers.
Jeudi 19 décembre 2024 à 20 heures
« Brève histoire des machines à calculer »
François Delannoy, membre de l'association Kafemath
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
Tout le monde a appris à effectuer une addition ou une multiplication à l'école, que ce soit mentalement
ou en posant l'opération. Comment élaborer un appareil mécanique permettant d'automatiser ce type de procédure mentale ?
Ce Kafemath sera l'occasion de découvrir une brève histoire des machines à calculer mécaniques.
Des inventions de Pascal et Schickard à celle de Curt Herzstark en passant par celles de Leibniz
et Thomas de Colmar. Ce voyage nous invitera à découvrir les raisons et les enjeux du développement
de ce domaine technique, à comprendre les principaux mécanismes mis en jeu et à manipuler
certaines de ces machines illustres.
Diaporama de l'exposé
Musée de l'Institut Henri Poincaré : Collection de machines à calculer
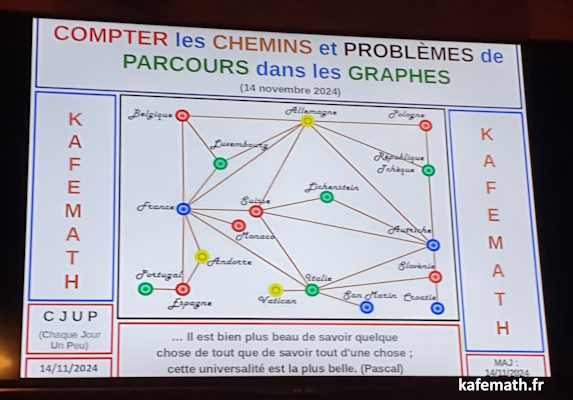
Jeudi 14 novembre 2024 à 20 heures
« Compter les chemins dans les graphes »
Christian Dufour, membre de l'association Kafemath
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
Une promenade sur les chemins du monde touffu des graphes ... ou comment s'initier à l'algorithmique du domaine : dénombrement à la Cayley-Prüfer, arbre couvrant, plus court chemin selon Dijkstra, etc
Lundi 21 octobre de 19 heures à 21 heures
« G4G : Gathering 4 Gardner »
Soirée animée par Pierre Berloquin
à "La Commune Libre d'Aligre", 3 rue d’Aligre, Paris 12ème.
Martin Gardner (1914-2010) était à la fois un mathématicien, un grand magicien, un illustre amateur de littérature et un esprit éclairé. L'association Kafemath honore depuis plusieurs années sa mémoire chaque 21 octobre, jour de sa naissance. L'événement se tient simultanément dans de nombreux pays, en liaison avec l'association américaine "Gathering For Gardner". Le temps d'une soirée pour rendre un hommage joyeux et jubilatoire à un personnage hors-normes !
- Avec les interventions de :
Philippe Boulanger - « Le biais du survivant »
Jean-Paul Delahaye - « Longues batailles et batailles infinies »
Christian Girard et Alain Zalmanski - « La Bible du palindrome »
Philippe Socrate - « Curiosités visuelles »
François Lavallou - « Le principe des tiroirs »
Jean Gagnerault - « Le jour de la semaine - Abaque de Kraitchik »
Edouard Thomas - « Les nouveaux pavages »
Vendredi 11 octobre 2024 de 20h à 21h30
« La vie et la théorie de Galois »
Hervé Stève, ingénieur mathématicien dans l'aéronautique, co-fondateur du Kafemath
Rencontre organisée par Intermines au Restaurant Ankara 11, rue du Molinel à Lille
Evariste Galois (1811-1832) est un mathématicien précoce engagé dans le mouvement républicain au lendemain
de la révolution de Juillet. Il est tué en duel à l'âge de 21 ans avant que son travail ait été reconnu.
Il est aujourd'hui considéré comme un génie en mathématique alors qu'il a été incompris à son époque.
Trouver les solutions générales des équations polynomiales a été un challenge pendant des siècles.
Voici un polynôme de degré n : p(x) = a0 + a1 x + a2 x2 + a3 x3 + a4 x4 + a5 x5 +... + an xn .
On a longtemps pensé que l'on pouvait le résoudre pour tout degré n, mais ce n'est pas le cas à partir
du degré cinq comme l'a montré Abel en 1824. Quelques années plus tard, Galois obtient le même résultat
en faisant intervenir une nouvelle structure : le groupe de Galois. Cette innovation permettra aux mathématiciens
des générations suivantes de trouver des applications en théorie des corps, en théorie des nombres, en géométrie
algébrique et même pour la démonstration du dernier théorème de Fermat (1995).
Lors de ce Kafemath, nous présenterons la biographie de Galois car même si sa vie a été courte celle-ci
a été bien remplie. Ensuite, nous retrouverons les solutions des équations polynomiales jusqu'au degré quatre
et nous montrerons les limites de la résolution pour les degrés supérieurs. Enfin, nous donnerons les définitions
du groupe de Galois, base de la théorie de Galois.
Jeudi 19 septembre 2024 à 20 heures
au café-bar "Aïre Ona" 1, rue du Docteur Goujon, Paris 12ème - Métro Daumesnil
« Dualité dans les polyèdres »
Julien Darrasse, membre de l'association Kafemath
« Triplets, de Pythagore à Eisenstein »
Jean Gagnerault, membre de l'association Kafemath
Quand les côtés d'un triangle rectangle sont mesurés par des nombres entiers,
on dit que ces trois nombres forment un triplet pythagoricien. De façon simple, on peut faire
apparaître les triplets pythagoriciens à partir du théorème de Pythagore et les triplets
d'Eisenstein à partir du théorème d'Al-Kashi. Ils font l'objet d'exercices
de programmation dans les cours d'algorithmique de niveau lycée.
De façon plus "complexe", ces triplets sont liés respectivement aux
entiers de Gauss et aux entiers d'Eisenstein. Après le remarquable Arbre de Berggren (1934),
quelques publications récentes apportent de nouveaux éclairages.
C'est un jeune prof de maths, rencontré lors d'un salon du CIJM place
St-Sulpice, qui m'a parlé des triplets d'Eisenstein. Qu'il en soit remercié !
retour Kafemath mise à jour : 27 juin 2025






.jpg)
 2.jpg)
 3.jpg)
.jpg)







.jpg)

.jpg)
.jpg)

.jpg)



 2.jpg)















.jpg)
.jpg)

 3.jpg)

.jpg)




.jpg)