Notre ami Jean-Louis Loday, mathématicien, directeur de recherche au CNRS, membre d'honneur de notre association, est décédé accidentellement au début du mois de juin 2012. Toutes nos condoléances à sa famille et à ses proches.

à "La Coulée Douce", 51 rue du Sahel, Paris 12 ième.

c'est mathématique à La Traverse le 02 juin 2012 après-midi à la libraire partenaire "La Traverse" 7, allée des Tilleuls, à La Courneuve (quartier de l'Hôtel de ville).
"Chiffres romains ... chiffres arabes", avec l'équipe du Kafemath...
Les chiffres romains et les chiffres arabes coexistent depuis des siècles. Les chiffres romains étaient utilisés de façon exclusive en France jusqu'au 13ième siècle... Chaque système de représentation des nombres a des avantages et des inconvénients ! En particulier, les opérations arithmétiques sont plus simples avec les chiffres arabes, mais traditionnellement, on regardait les résultats à l'aide d'"abaques". Pourtant, en obligeant à nommer le vide avec le nombre zéro, une invention proposée entre autres par l'Indien Brahmagupta dès le 7ième siècle, les chiffres arabes ont introduit le chiffre zéro dans la représentation des nombres, ouvrant la voie à des progrès conceptuels essentiels.

au "Moulin à Café", 9 place de la Garenne, Paris 14 ième.
Les nombres premiers, qui sont des entiers naturels qui n'ont comme diviseurs 1 ou eux-mêmes,
ne sont pas les premiers des nombres mais sont présents depuis l'antiquité (Babyloniens, Egyptiens) et peut-être depuis la préhistoire avec l'os d'Ishango (-20 000 a.J.C.), mais c'est dans les éléments d'Euclide (-300 a.J.C.) que l'on trouve leur définition, la preuve de leur infinité et les algorithmes pour les trouver. Comme il y a beaucoup de choses à dire sur les nombres premiers, on abordera dans ce Kafemath les notions les plus basiques et accessibles au plus grand nombre. Après quelques rappels sur les nombres entiers, les diviseurs, on démontrera ensemble le théorème fondamental de l'arithmétique en faisant mieux connaissance avec Euclide. Quelques années plus tard un autre Grec Erastosthène popularisera les nombres premiers avec son fameux crible. On verra ensuite quelques propriétés sur les nombres premiers. Puis on s'intéressera à Pierre de Fermat (17ème) et en particulier à son "petit théorème" démontré plus tard par Léonard Euler.

à "L'Oiseau Blanc", 19 rue de Rome, Paris 8 ième, métro Saint-Lazare.
La démocratie repose sur des élections libres... Et le processus de vote consiste à agréger des opinions individuelles pour constituer un choix social effectif. Cette question en apparence anodine conduit en fait à une difficulté mathématique quasi-inextricable puisque le problème n'a essentiellement pas de solution. Nous revisiterons sur un exemple la question du paradoxe de Condorcet (1785) et surtout son impossible résolution via les travaux du mathématicien Arrow (1950). Nous montrerons, en les pratiquant lors de la séance, que des idées récentes comme le vote par assentiment ou le vote majoritaire de Balinski et Laraki (2006) proposent des approches à peine plus complexes que les systèmes existants mais et demandent au citoyen une prise de position sur chaque candidat. Un système probablement encore plus démocratique que le vote à deux tours !

à "La Coulée Douce", 51 rue du Sahel, Paris 12 ième.
Les citoyens, les médias, et les acteurs politiques se servent des sondages politiques, et plus particulièrement des enquêtes d'intentions de vote, comme d'instruments de prévision électorale. D'un point de vue statistique, un sondage correspond à l'étude des méthodes permettant de sélectionner un échantillon à partir d'une population finie,
aux méthodes d'amélioration des estimations et aux méthodes de calcul des variances d'échantillonnage. Ces méthodes sont généralement exposées dans le cadre théorique d'un modèle où chaque individu sélectionné dans l'échantillon peut être joint et accepte de répondre à l'enquête (absence d'erreur de non-réponse), puis sait répondre, accepte de répondre aux questions posées et donne la vraie réponse (absence d'erreur de mesure). Dans ce contexte, le seul type d'erreur qui affecte les résultats est l'erreur d'échantillonnage, c'est-à-dire la différence entre la valeur du paramètre étudié sur la population tout entière et la valeur du paramètre estimé sur l'échantillon sélectionné. Cependant en pratique, il y a beaucoup d'autres sources d'erreur. Après un rappel rapide des notions de base d'un point de vue statistique,
nous essayerons de présenter les différentes sources d'erreur pouvant affecter
la qualité des enquêtes et des méthodes possibles pour les prévenir et/ou y remédier. Le but de cet exposé est donc de permettre aux utilisateurs de données d'enquête d'en évaluer la qualité.

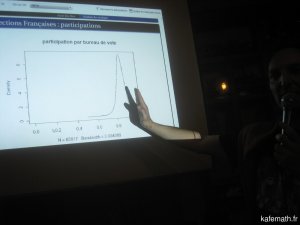
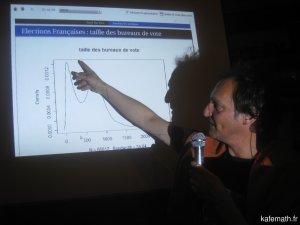
Pour en savoir plus, on pourra consulter l'article d'Avner Bar-Hen et Jean Chiche Les sondages sont-ils devenus fous ? sur le site "Images des Mathématiques".

Comment on a inventé les nombres imaginaires.
En cherchant des racines aux équations du troisième degré,
un mathématicien italien de la Renaissance, Rafaelle Bombelli,
a osé braver un interdit absolu : les racines de nombres négatifs.
Ou comment un nouveau concept s'impose aux humains, alors qu'ils ne le cherchaient pas.
Pire, qu'ils s'en seraient bien dispensés !... Enfin, toute la richesse que cette précieuse pépite a apporté dans de nombreux domaines de la physique et des maths elles-mêmes.

Au panthéon des figures remarquables de l'histoire des sciences trône le mathématicien Srinivasa Ramanujan (1887-1920). Personnage romantique, à la destinée tragique, cet autodidacte passionné, issu d'une famille indienne modeste, est l'auteur de découvertes inédites et profondes en analyse. Ses résultats sont consignés dans des carnets, sous la forme de milliers de formules, qui sont autant d'énigmes mathématiques. En près de cent ans, aidés parfois de moyens de calculs et de théories sophistiquées inexistants à l'époque du prodige indien, les mathématiciens ont réussi à décrypter et prouver la plupart de ses formules. Ce travail d'édition des carnets de Ramanujan, l'un des plus colossaux de l'histoire des sciences, est encore inachevé. Lorsqu'il aura été mené à terme, l'étendue de l'œuvre de ce mathématicien atypique sera révélée. Mais il restera à résoudre une dernière énigme, la plus mystérieuse de toutes : d'où provenait l'intuition du prodige indien ?

Les codes nous accompagnent depuis des millénaires.
Avec eux, nous avons construit nos mathématiques et nos sciences,
nous avons défini nos religions, nos morales et nos goûts artistiques.
Mais depuis le XXème siècle, les codes ne sont plus de simples outils passifs
comme le marteau, la règle ou le compas.
Ils deviennent peu à peu actifs, au point d'acquérir leur autonomie.
Suivons donc ensemble, de Pythagore à nos jours, les événements et les hommes
qui ont porté les codes et les ont développés.

Les fractales sont des figures géométriques découvertes au début du 20 ième siècle
qui ont cette curieuse propriété qu'après une transformation convenable, on retrouve exactement l'ensemble de la figure... Elles ont été popularisées avec le travail de Benoît Mandelbrot et son fameux "ensemble de Mandelbrot".
Dans son exposé, Hervé nous montre comment la notion de dimension
(un pour une droite, deux pour un plan, etc) peut se généraliser à des figures fractales.

La Commune libre d'Aligre animé par Pierre Berloquin.
Avec quelques divertissements "à la Martin Gardner"            
Magies non standard (Pierre Berloquin),
Enveloppes (Philippe Boulanger),
Morpion solitaire (Christian Boyer),
Découpages de Kimmo Eriksson (Michel Criton),
Le tour de cartes d'Abdul Alafrez (François Dubois),
Principes nouveaux en magie (Christian Girard),
Une lecture de "Logique sans peine" de Lewis Carroll (Béatrice L.),
Cubes magiques et mnémotechnies selon Charles Barbier (Benoît Rosemont),
Ferryboat problem (Blandine Sergent),
Docteur Matrix (Alain Zalmanski).

"Le Goût des Sciences - les scientifiques communiquent"
remis le 11 octobre 2011 au Musée du quai Branly.

Au Japon, pendant l'ère Edo, d'ingénieux habitants, du peuple jusqu'aux samourais, disposent leur trouvailles mathématiques sous forme de belles tablettes votives, les sangakus, dans les temples shintoistes et bouddhistes. Elles vont constituer l'apport local aux mathématiques durant cette longue période de fermeture quasi-totale du Japon. La présentation est dans le droit fil de l'esprit Kafémath, mêlant art, histoire, sacré, poésie, et mathématiques bien sûr!

au "Forum des Associations du douzième arrondissement", boulevard de Reuilly.