Introduction

    Techniques graphiques de
 résolution de problèmes





Abaque



Avantages/Inconvénients

    1) Calcul par le trait
   ... on construit
   
2) Abaques (ou Nomogrammes)
   ... on lit
  
   
Diagramme rassemblant des
    résultats calculés à l'avance


Evite des calculs répétitifs 

Précision limitée

Faible coût de fabrication

Facilité d'utilisation

    Plan

    Bases de la théorie



Méthode géométrique



Méthode analytique




Exemples pratiques


Evolution de la théorie



Conclusion


    Fondateurs
Exemple : Fonction z = x.y 


Coordonnées parallèles
Dualité projective


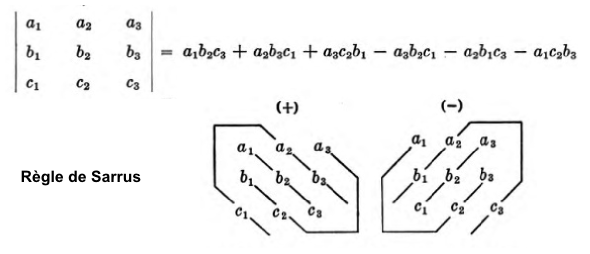
Déterminants
Equation d'une droite
Etapes de construction
Equation z3 + pz + q = 0




Développements complémentaires
Diffusion internationale
Les abaques aujourd'hui ?

Retour vers z = x.y

    Louis-Ezéchiel Pouchet (1748-1809)

    
Faisceau d'hyperboles

a = 4
b = 5

c = a x b = 20

    Léon-Louis Lalanne (1811-1892)

    
Droites concourantes

Anamorphose géométrique

Echelles fonctionnelles
log(c) = log(a) + log(b)

a = 4
b = 5

c = a x b = 20

    Maurice d'Ocagne (1862-1938)

    

Points alignés

a = 4
b = 5

c = a x b = 20

    Junius Massau (1852-1909)

    
Anamorphose généralisée

La relation F(x,y,z) = 0 est représentable par un abaque 
à droites concourantes si, et seulement si, il existe 
des fonctions d'une seule variable f1, f2, f3, g1, g2, g3, 
h1, h2, h3 telles que



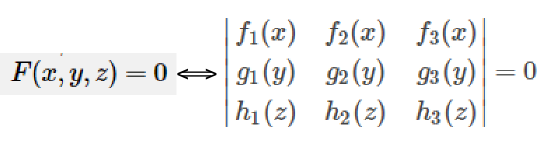Ce déterminant est appelé Déterminant de Massau

    Coordonnées parallèles - 1 : La droite

    

Ligne de base AB

Axes Au et Bv


Coordonnées
de la droite MN :

u = AM, v = BN

    Coordonnées parallèles - 2 : Le point

    

Point fixe P
Droite variable MN

On pose :
AA'= a, BB'= b

Coordonnées de MN :
AM = u, BN = v


Equation du point P : 
u/a + v/b - 1 = 0

    Dualité projective

    


     

     

    Déterminants

    Equation d'une droite

    


     

     

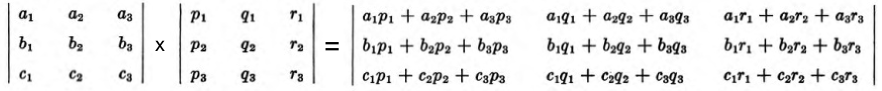
    Abaque à points alignés : Principe

    Construction d'un abaque à points alignés - 1

    

Etape (1) 


Disjoindre les variables


Déterminant de Massau

    Construction d'un abaque à points alignés - 2

    

Etape (2)


Mettre en forme
le déterminant

Les éléments de D 
sont des constantes

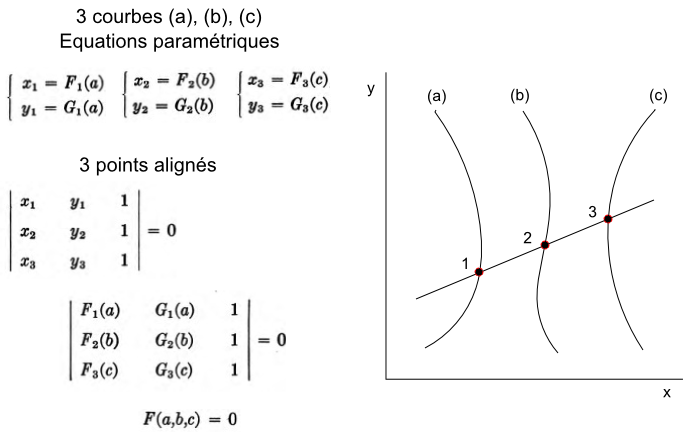
    Construction d'un abaque à points alignés - 3

    

Etape (3)


Tracer les courbes
(a), (b), (c) 
 
cotées selon les 
valeurs a, b, c

    Equation z3 + pz + q = 0

    Equation z3 + pz + q = 0

    

Exemple : z3 - 7z + 6 = 0 (1)

Racines positives : 1 et 2
Joindre p=-7 et q=+6

Racine négative : -3 
Joindre p=-7 et q=-6


En changeant z en -z,
on obtient z3 - 7z - 6 = 0 (2)

Les racines positives de (2)
sont aussi les racines 
négatives de (1)

    Exemples - Cliquer sur l'image pour l'agrandir


    Compteur universel



    Le Triomphe (1)



    Le Triomphe (2)



    x = a + b + c + d





    Surface corporelle



    1/x1 + 1/x2 = 1/x



    Temps d'usinage



    Quadripôle

    Evolution de la théorie

    
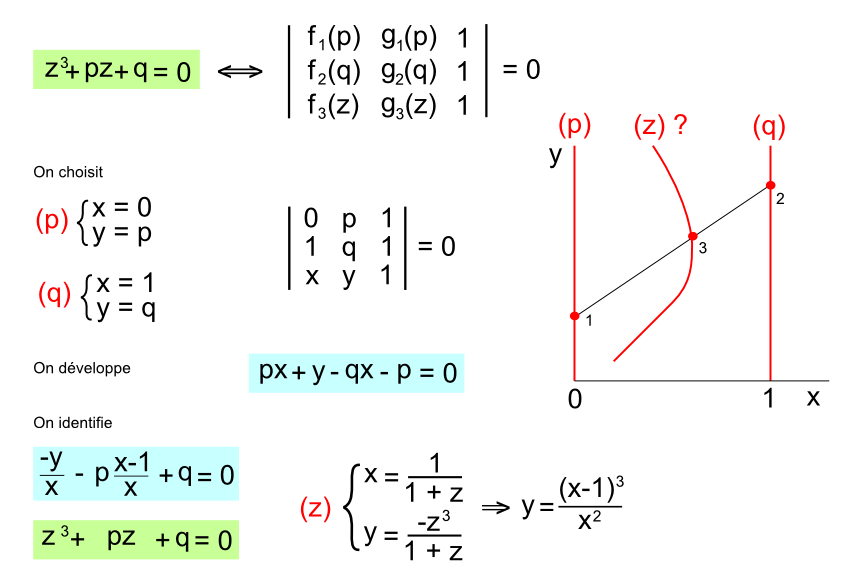
Développements complémentaires

    Ingénieurs : Lallemand, Soreau ...
	
Mathématiciens : Clark, Gronwall ...


Diffusion internationale

Allemagne, URSS ...


Les abaques aujourd'hui ?